En matemáticas, un patrón se refiere a una secuencia regular o repetitiva de números, formas u otros objetos matemáticos. Un patrón se puede describir usando una fórmula o regla que genera el patrón y, a menudo, se puede extender para continuar la secuencia o encontrar ejemplos adicionales del patrón.
Los patrones son importantes en muchas áreas de las matemáticas, incluidas el álgebra, la geometría y la teoría de números. Se pueden usar para hacer predicciones, identificar relaciones entre diferentes objetos matemáticos y encontrar soluciones a problemas. El estudio de patrones a menudo se denomina teoría de patrones y es una parte importante de la investigación y la educación matemática en todos los niveles.
Reglas de patrón
Un patrón se puede describir mediante un conjunto de reglas que generan la secuencia o el objeto de manera predecible y consistente. Las reglas específicas de un patrón pueden variar según el tipo de patrón, pero algunas reglas comunes que pueden seguir los patrones incluyen:
- Un patrón numérico puede seguir una progresión aritmética o geométrica específica.
- Un patrón de forma puede seguir una regla específica de simetría o mosaico.
- Un patrón de secuencia puede seguir un algoritmo específico o una fórmula recursiva.
Estas reglas se pueden usar para predecir el siguiente término u objeto en el patrón, o para generar ejemplos adicionales del patrón. Al analizar patrones, es importante buscar regularidades e identificar las reglas subyacentes que gobiernan el patrón. Esto a menudo puede proporcionar información sobre la estructura matemática del patrón y conducir a nuevos descubrimientos y aplicaciones.
Tipos de patrones
Hay varios tipos de patrones en matemáticas. Algunos tipos comunes incluyen:
Patrones Numéricos: Estos son patrones que involucran una secuencia de números que siguen una regla específica. Por ejemplo, la secuencia de Fibonacci es un patrón numérico donde cada término es la suma de los dos términos anteriores.
Patrones Geométricos: Estos son patrones que involucran una secuencia de formas o figuras que siguen una regla específica. Por ejemplo, una teselación es un patrón geométrico formado por formas repetitivas que encajan entre sí sin espacios.
Patrones Fractales: Estos son patrones que tienen auto-similitud en diferentes escalas. Los patrones fractales se pueden encontrar en la naturaleza, como en los patrones de ramificación de los árboles y la forma de los copos de nieve.
Patrones de simetría: estos son patrones que tienen simetría, lo que significa que se pueden dividir en partes que son imágenes especulares entre sí. Los ejemplos de patrones de simetría incluyen caleidoscopios y copos de nieve.
Patrones algorítmicos: son patrones generados por un algoritmo específico o un conjunto de reglas. Por ejemplo, la curva de Koch es un patrón algorítmico que se crea agregando repetidamente segmentos más pequeños a los lados de un triángulo.
Patrones periódicos: estos son patrones que se repiten durante un intervalo fijo. Los ejemplos de patrones periódicos incluyen las estaciones y las fases de la luna.
Estos son solo algunos ejemplos de los muchos tipos diferentes de patrones en matemáticas. Identificar y analizar patrones es una parte importante del pensamiento matemático y la resolución de problemas.
Ejemplos de patrones
Hay muchos ejemplos de patrones en matemáticas. Estos son algunos ejemplos comunes:
Secuencia de Fibonacci: Este es un patrón numérico donde cada término es la suma de los dos términos anteriores. La secuencia comienza con 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 y así sucesivamente.
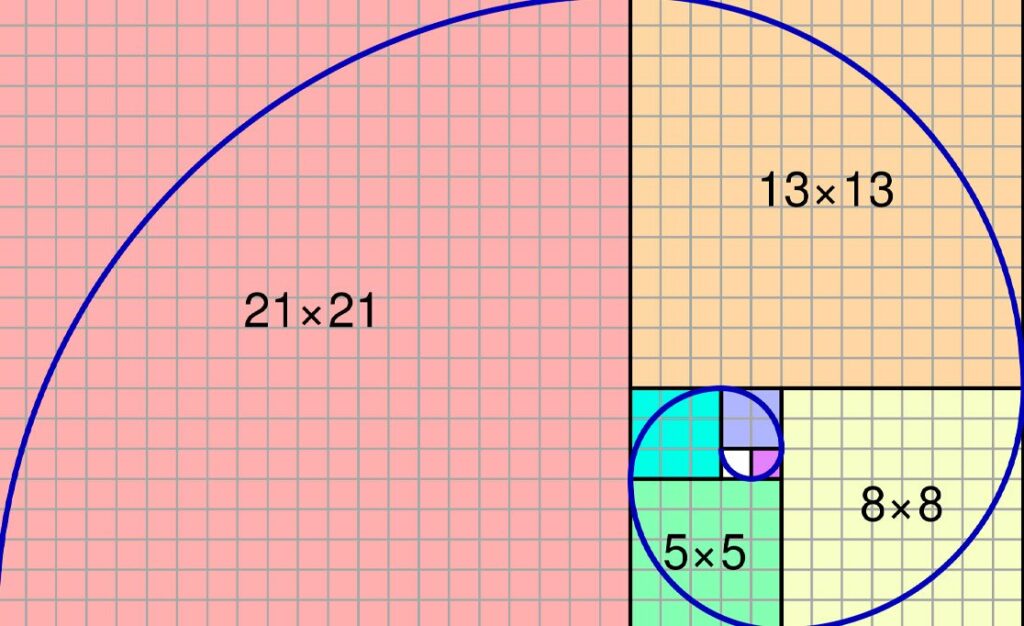
Teselaciones: Estos son patrones geométricos hechos de formas repetitivas que encajan juntas sin espacios. Los ejemplos incluyen las teselaciones regulares formadas por triángulos equiláteros, cuadrados y hexágonos.

Triángulo de Sierpinski: este es un patrón fractal que se crea quitando repetidamente un triángulo más pequeño del centro de un triángulo equilátero más grande. El patrón es autosimilar a diferentes escalas y tiene un número infinito de niveles.

Patrones de simetría: estos son patrones que tienen simetría, lo que significa que se pueden dividir en partes que son imágenes especulares entre sí. Los ejemplos incluyen la simetría de reflexión de las alas de una mariposa y la simetría de rotación de un copo de nieve.

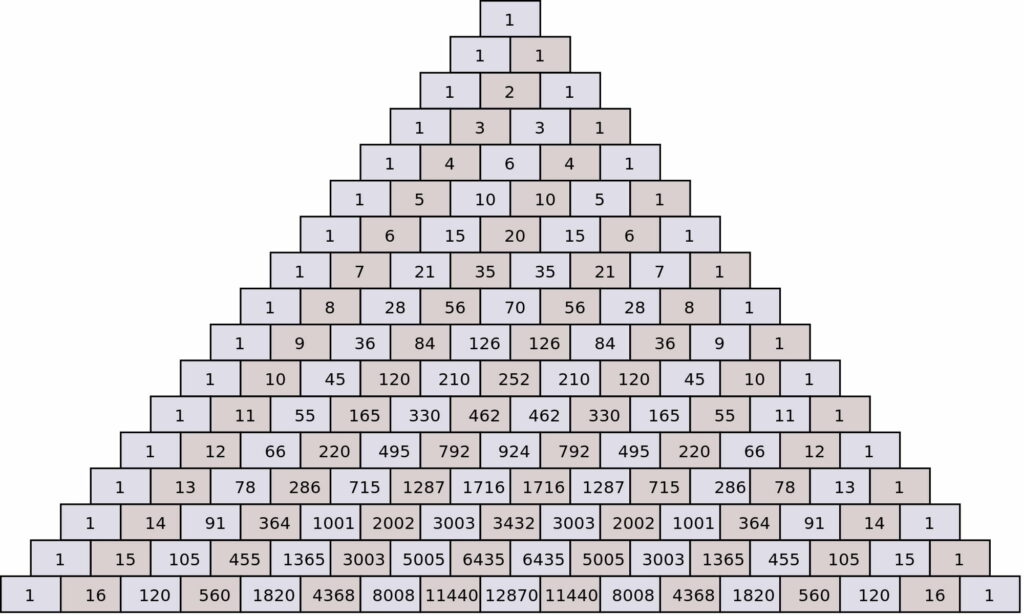
Triángulo de Pascal: este es un patrón numérico que se crea al sumar los dos números sobre cada término para obtener el siguiente término. El patrón comienza con la fila 1, 1, 1, 1, 2, 1, 1, 3, 3, 1, y así sucesivamente.
Conjunto de Mandelbrot: este es un patrón fractal que se crea aplicando repetidamente una fórmula matemática compleja a cada punto en un plano. El patrón resultante tiene detalles intrincados y es similar a sí mismo en diferentes escalas.

Estos son solo algunos ejemplos de los muchos tipos diferentes de patrones en matemáticas. Identificar y analizar patrones es una parte importante del pensamiento matemático y la resolución de problemas.